2025 CSDMS meeting-102

Edit registration

Pay registration

(if you haven't already)

Log in (or create account for non-CSDMS members)
Forgot username? Search or email:CSDMSweb@colorado.edu

Browse  abstracts

<<

>>

Back to meeting

Theoretically and Empirically based modeling of the evolution of multi-species marshes

Brad Murray, (he/him),Duke University Durham North Carolina, United States. abmurray@duke.edu

Conner Lester, Duke University Durham North Carolina, United States. conner.lester@duke.edu

Morgan Alexander, Duke University , United States.

Nathaniel Blackford, Duke University , United States.

Andrea D'Alpaos, University of Padova Padova , Italy.

Orencio Duran, Texas A&M University , United States.

Marco Marani, University of Padova , Italy.

Tegan Blount, University of Padova , Italy.

Dani Rubio, Duke University , United States.

Sonia Silvestri, University of Bologna , United States.

Zhicheng Yang, Duke University (now at University of Georgia) , United States.

We have developed a simple approach to modeling how coastal marshes respond to changes in the rate of sea level rise (SLR) and sediment concentration. This approach, rooted in detailed numerical modeling and in field and remotely sensed observations, produces plan view distributions of elevations and the densities of multiple marsh species and bare soil. This modelling approach can be applied to specific marshes, to forecast marsh configurations for any combination of SLR rate and suspended sediment concentration in a channel network.

The approach involves techniques to detect the spatial distributions of fractional cover and biomass densities of multiple marsh species from satellite observations. These techniques were developed using a combination of field observations and drone and airborne lidar and multispectral data from the East Coast of the United States and the Venice Lagoon, and can be applied to any coastal environment with similar mixes of vegetation types. Biomass density can be treated as a function of elevation, representing the realized niches of observed vegetation species, or mixtures of species.

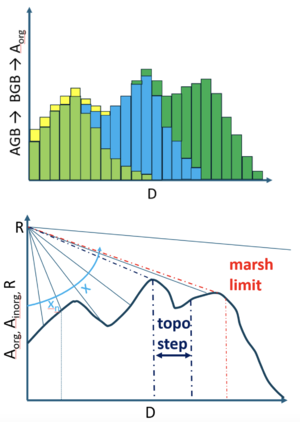
The approach also involves modeling demonstrating that, within marsh basins, tidal current velocities and rates of inorganic sediment deposition do not depend on vegetation properties. Given this simplification, and the relationship between biomass density and elevation (realized niches), solving for equilibrium depths and biomass densities as a function of distance from the nearest channel becomes straightforward (Figure 1).

The rate of change of depth D (below high-water level) is given by:

∂D/∂t = R - A_inorg - A_org

where R is the rate of SLR, A_inorg and A_org are the rates of accretion of inorganic and organic sediment, respectively. A_inorg is equal to DC, where C is sediment concentration. In Figure 1, equilibrium depths (∂D/∂t=0; R - A_inorg = A_org) are graphically determined.

Acknowledgments

Supported by the US NSF Geomorphology and Land Use Dynamics program (2016068), and AA, MM, and SS were also supported by the RETURN Extended Partnership and received funding from the European Union Next-GenerationEU (National Recovery and Resilience Plan – NRRP, Mission 4, Component 2, Investment 1.3 – D.D. 1243 2/8/2022, PE0000005).

Figure 1: (Top) Hypothetical relationship between A_org (proportional to biomass density) and D for multiple species (different colors) and mixtures of species. (Bottom) Graphical representation of equilibria in Equation (1) for some future R. Slanting lines represent A_inorg at different nondimensional distances from a channel (with C decreasing with distance from a channel). Intersections between the slanting lines and the curve represent equilibrium depths at different distances from a channel. Sections of the curve that are not intersected by slanting lines represent topographic steps and abrupt vegetation zonation. (Equilibria are unstable when the local slope of the curve is more negative than the slope of the intersecting line.)