Model help:GIPL

GIPL
GIPL is a heat flow with phase change model use to model permafrost thermal state and active layer depth, can be used for site specific and regional ground temperature distribution modeling.
Model introduction
GIPL(Geophysical Institute Permafrost Laboratory) is an implicit finite difference transient one-dimensional heat flow model. The model simulates ground temperature dynamics and the depth of the active layer by solving non-linear heat equation with phase change numerically. The model employs the Enthalpy method which does not require explicit treatment of the freeze/thaw moving boundary. In this model the process of freezing or thawing is occurring in accordance with unfrozen water content and soil thermal properties, and depends on the degree of soil saturation.
Model parameters
Input files and Directories
| Parameter | Description | Unit |
|---|---|---|
| Switcher | 1 runs new simulation reading initial temperature distribution from initial.txt file in input folder, 0 continues simulation by reading initial temperatures from dump/start_001.txt file | - |
| Output time step | Output calculated temperatures based on output time step input. For example, 1 correspond to 1 day time interval. The result.txt file has the temperature distribution output based on the output time interval. | days |
| Calculation step | Calculation time step used in Stefan subroutine. | - |
| Minimal time step | Minimum time step is a constrain for calculation time step used in Stefan subroutine. | - |
| Number of years | If the number is greater than 1 then the model simulates the ground temperature distribution and write mean annual temperature distribution with depth into mean_001.txt file. | years |
| Max distance between next temperature
iterations (E1) (0.001-0.1) |
If the absolute difference between current and next temperature iteration is greater than E1 then apply sweep method (see Ismayil-zadeh and Tackley 2010) over again. Used in Stefan subroutine. | - |
| Error of saturation for next iteration (UWK) | If the absolute difference between current and next saturated unfrozen water coefficient is greater than UWK then apply sweep method over again. Used in Stefan subroutine. | - |
| Max number of iterations before dividing time step | If the current and next temperature iteration do not converge i.e. absolute difference is greater than E1 then time step divided by 2. Used in Stefan subroutine. | - |
| Number of seconds per step | For output time step 1 day number of seconds is equal to 86400. | sec |
| Average number | The average number of days in one year 365. | day |
| depth of earth surface | meters | |
| maximum number of freezing fronts | For example if there case of a talik there are more than 2 freezing fronts | - |
| min depth of freezing front | meters | |
| max depth of freezing front | meters | |
| The saturation coefficient | Used for freeze/thaw front calculation | percent |
GIPL INPUT FILES
Boundary Input Files and Grid
| Input Data | Description | Unit | File Name |
|---|---|---|---|
| The upper boundary file | Time series of the temperature, usually air temperature. The default file include daily temperature distribution. First number correspond to number of variables. The right column correspond to number of day. The left column correspond to daily temperature. | days|<math>^oC</math> | upbound.txt |
| The snow depth file | Time series of the snow depth. The default file include daily snow depth. First number correspond to number of variables. The right column correspond to number of day. The left column correspond to daily snow depth. | days|meters | snow.txt |
| The snow conductivity file | Time series of the snow conductivity. The default file include daily snow conductivity. First number correspond to number of variables. The right column correspond to number of day. The left column correspond to daily snow conductivity. | days|W/(mK) | rsnow.txt |
| The grid file | The default file include number of grid points from 1.5m above the surface to 33 m depth below and id number of the output points. | meters | grid.txt |
| Initial temperature distribution file | The first number in the file correspond to point id, the second to the number of temperature points | meters | initial.txt |
Thermo-Physical Properties Files
| Input Data | Description | Unit | File Name |
|---|---|---|---|
| Thermo-physical properties of the mineral soil layers | Number of classes. Class id and number of layers in the class. Each layer has its own volumetric water content(%), a and b empirical coefficients(dimensionless), thawed and frozen volumetric heat capacities (<math>Jm^{-3}K^{-1}</math>), thawed and frozen thermal conductivities(<math>Wm^{-1}K^{-1}</math>), depth of the corresponding layer(m). | - | mineral.txt |
| Thermo-physical properties of the upper organic layers | See thermo-physical properties of the mineral soil layers description | - | organic.txt |
| The input file | The input file includes: number of simulation point (default "1"), id of the first point, number of the point's snow class, vegetation class, mineral soil class, initial temperature profile class and the corresponding geothermal heat flux at the lower boundary. | - | input.txt |
Uses ports
This will be something that the CSDMS facility will add
Provides ports
This will be something that the CSDMS facility will add
Main equations
1) Heat Flow Equation
<math> \frac{\partial H(x,t)}{\partial \tau}=\texttt{div}(k(x,t)\nabla t(x,\tau)) </math> (1)
where <math>x\in(l_1,l_2)</math> is a spatial variable which changes with depth and <math>\tau\in(0,T]</math> is a temporal variable.
2) The Enthalpy Formulation
<math> H(x,t)=\int\limits_0^tC(x,s)ds+L\Theta(x,t) </math> (2)
3) The upper boundary condition
<math> t(l_1,\tau)=t_{air}</math> (3)
4) The lower boundary condition
<math> \frac{\partial t(l_2,\tau)}{\partial x}=g</math> (4)
5) The initial temperature distribution
<math> t(x,0)=t_0(x)</math> (5)
6) The unfrozen water content <math>\Theta(x,t)</math>:
<math> \Theta(x,t)=\eta(x)\cdot\begin{cases} 1 , & t\ge t_* \\ a|t|^{-b}, & t< t_* \end{cases} </math>
(6)
Notes
Numerical scheme
Examples
An example run with input parameters, BLD files, as well as a figure / movie of the output
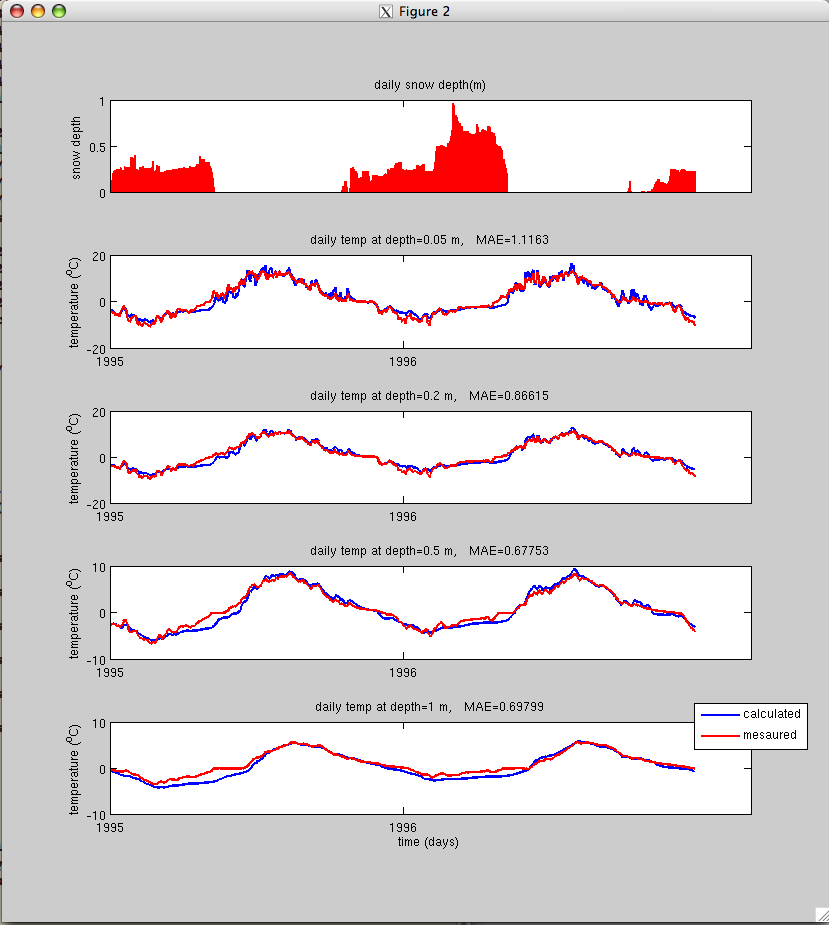 Follow the next steps to include images / movies of simulations:
Follow the next steps to include images / movies of simulations:
- Upload file: https://csdms.colorado.edu/wiki/Special:Upload
- Create link to the file on your page: [[Image:<file name>]].
See also: Help:Images or Help:Movies
Developer(s)
Name of the module developer(s)
References
Ismail-Zadeh A, Tackley P. 2010. Computational Methods for Geodynamics. Cambridge.
Links
Any link, eg. to the model questionnaire, etc.
