Meeting:Abstract 2013 CSDMS meeting-030
Browse abstracts
A Mophodynamic Explanation for the Shoreface Depth of Closure
[[Image:|300px|right|link=File:]]This research aims to understand the evolution of the shoreface of sandy, wave-dominated coasts. Using energetics-based formulations for wave-driven sediment transport, we develop a robust methodology for estimating the morphodynamic evolution of a cross-shore beach profile. We compare how shallow water wave assumptions and linear Airy wave theory affect the estimation of morphodynamic shoreface evolution, in contrast to previous work, which has applied shallow water wave assumptions across the entire shoreface. The derived cross-shore sediment flux formula enables the calculation of a steady state (or dynamic equilibrium) profile based on three components of wave influence on sediment transport: two onshore-directed terms (wave asymmetry and wave drift) and an offshore-directed slope terms. Equilibrium profile geometry depends on wave period and grain size. The profile evolution formulation yields a morphodynamic Péclet number that can be analyzed in terms of perturbations around the steady-state profile. The diffusional, offshore-directed slope term dominates long-term profile evolution. A depth-dependent characteristic timescale of diffusion allows the estimation of an effective morphodynamic depth of closure for a given time envelope. Theoretical modeled computations are compared to four field sites along the Eastern US coastline. For each of these four field sites, we use hindcast wave data to determine a representative wave height and period using a weighted frequency-magnitude approach. Using the characteristic wave quantities for each site, we compute the equilibrium profile and the morphodynamic depth of closure, showing reasonable similarities between the computed equilibrium profiles and the actual profiles. In addition, the estimated morphodynamic depth of closure matches well with the location of the visually estimated depth of closure (based upon slope break) for each site. Overall, the methodology espoused in this paper can be used with relative ease for a variety of sites and with varied sediment transport equations.
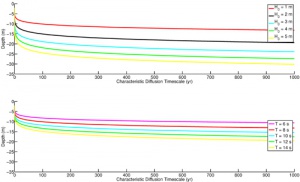 |
| Modeled characteristic timescale of diffusivity using linear theory over depth with varying (a) deep-water wave height with T =8 s and (b) varying wave period with H0 = 1 m. |
