Labs Landscape Evolution Modeling With Child Part 2
Landscape Evolution Modeling with CHILD
Part 2: Rainfall, runoff and drainage networks and hydraulic geometry
Gregory E. Tucker, University of Colorado Boulder, and Stephen T. Lancaster, Oregon State University
Before beginning these exercises, please download the CHILD visualization tools here: File:CHILDVisTools.tar.gz.
Rainfall, Runoff, and Drainage Networks
In order to calculate erosion, sediment transport, and deposition by running water, a model needs to know how much surface water is flowing through each cell in the model. Usually, the erosion/transport equations require either the total discharge, Q [L3/T], the discharge per unit channel width, q [L2/T], or the flow depth, H.
There are three main alternative methods for modeling the flow of water across the landscape:
Methods based on contributing drainage area
Numerical solutions to the 2D, vertically integrated and time-averaged Navier-Stokes equations
Cellular automaton methods
Methods Based on Drainage Area
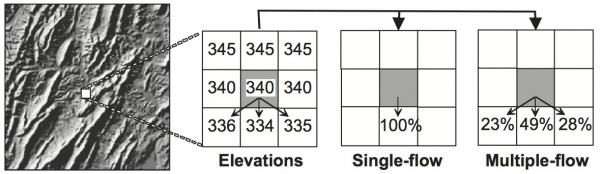
Drainage area, A, is the horizontally projected area of land that contributes flow to a particular channel cross-section or to unit length of contour on a hillslope. For a numerical landscape model that uses discrete cells, A is defined as the area that contributes flow to a particular cell. When topography is represented as a raster grid, the most common method for computing drainage area is the D8 method. Each cell is assigned a flow direction toward one of its 8 surrounding neighbors. An algorithm is then used to trace flow paths downstream and add up the number of cells that contribute flow each cell (Fig. 3).
For the Voronoi cell matrix that CHILD and CASCADE use, the simplest routing procedure is a generalization of D8 (Fig. 1). Each cell i has Ni neighbors. As we noted earlier, the slope from cell i to neighbor cell k is defined as the elevation difference between the nodes divided by the horizontal distance between them (Fig. 2). Thus, one can define a slope for every edge that connects each pair of nodes. There is a slope value for each of the Ni neighbors of node i. The flow direction is assigned as the steepest of these slopes.
Single-direction flow algorithms have advantages and disadvantages. Some models use a multiple flow direction approach to represent the divergence of flow on relatively gentle slopes or divergent landforms (Fig. 3). This is most appropriate for models that operate on a grid resolution significantly smaller than the length of a hillslope. When grid cells are relatively large, conceptually each cell contains a primary channel, narrower than the cell, that is tracked.
Exercise 4: Flow Over Noisy, Inclined Topography
>> In WMT, go to the public labls and open the model titled "Network1." Save and submit the job.
>> Download the results and move them to the folder childFolderLocation∖ChildExercises∖network1. For childFolderLocation, use the path to the Child visualization tools package that you downloaded.
>> In Matlab, navigate to the network1 folder. Type:
- figure(1), clf
- colormap pink
- a = cread( 'network1.area', 1 );
- ctrisurf( 'network1', 1, a );
- view( 0, 90 ), shading interp, axis equal
The networks are formed because of noise (<math>\pm 1</math> m in this case) in the initial surface, which causes flow to converge in some places.
The simplest method for computing discharge from drainage area is to simply assume (1) all rain runs off, and (2) rain lasts long enough that the entire drainage network is in hydrologic steady state. In this case, and if precipitation rate P is uniform,
A number of landscape modeling studies have used this assumption, on the basis of its simplicity, even though it tends to make hydrologists faint! The simplicity is indeed a virtue, but one needs to be extremely careful in using this equation, for at least three reasons. First, obviously Q varies substantially over time in response to changing seasons, floods, droughts, etc. We will return to this issue shortly. Second, there is probably no drainage basin on earth, bigger than a hectare or so, from which all precipitation runs off. Typically, evapotranspiration returns more than half of incoming precipitation to the atmosphere. Third, hydrologic steady state is rare and tends to occur only in small basins, though it may be a reasonable approximation for mean annual discharge in some basins.
River discharge, whether defined as mean annual, bankfull, mean peak, or some other way, often shows a power-law-like correlation with drainage area. Some models take advantage of this fact by computing discharge using an empirical approach:
where c typically ranges from 0.5-1 and b is a runoff coefficient with awkward units that represents a long-term “effective” precipitation regime.
CHILD’s default method for computing discharge during a storm takes runoff at each cell to be the difference between storm rainfall intensity P and soil infiltration capacity I:
which of course is taken to be zero when P < I.
Shallow-Water Equations
Some landscape models are designed to address relatively small-scale problems such as channel initiation, inundation of alluvial fan surfaces, channel flood flow, etc. In such cases, the convergence and divergence of water in response to evolving topography is an important component of the problem, and is not adequately captured by the simple routing schemes described above. Instead, a tempting tool of choice is some form of the shallow-water equations, which are the vertically integrated form of the general (time-averaged) viscous fluid-flow equations. One form of the full shallow-water equations is:
\frac{\partial \eta}{\partial t} = i - \left( \frac{\partial q_x}{\partial x}
+ \frac{\partial q_y}{\partial y} \right ) </math> (14)+ \frac{\partial q_y u}{\partial y} + g h \frac{\partial h}{\partial x} + g h \frac{\partial \eta}{\partial x}
+ \frac{\tau_{bx}}{\rho} = 0 </math> (15)+ \frac{\partial q_x v}{\partial x} + g h \frac{\partial h}{\partial y} + g h \frac{\partial \eta}{\partial y}
+ \frac{\tau_{by}}{\rho} = 0</math> (16)These equations express continuity of mass, x-directed momentum, and y-directed momentum, respectively. They are challenging and computationally expensive to integrate numerically in their full form. However, there are several approximate forms that are commonly used, including the non-accelerating flow form (in which convective accelerations are assumed negligible) and the kinematic-wave equations (in which gravitational and friction forces are assumed to dominate). An example of use of the shallow-water equations in a landform evolution model can be found in the work of T.R. Smith and colleagues (Fig. 4). Various forms of the shallow-water equations can often be found in hydrologic models, and sometimes in soil-erosion models (e.g., Mitas and Mitasova 1998).
Cellular Automata
Some models use cellular automaton methods to calculate flow over a cellular topography. These include:
Chase (1992) precipiton algorithm
Crave and Davy (2001) modified precipiton algorithm
Murray and Paola (1994) multiple-flow-direction river-flow algorithm
Coulthard, Kirkby, and Macklin (1996) generalization of Murray-Paola for 2D flow (CAESAR model)
Depressions in the Terrain
What happens when flow enters a topographic depression? In the real world, three possibilities: complete evaporation/infiltration, formation of a lake with overflow, or formation of a closed lake. CHILD can be set either to have water in “pits” evaporate, or to use a lake-fill algorithm to route water through depressions in the terrain (with no evaporation).
Precipitation and Discharge
Water supply to the channel network varies dramatically in both time and space, but there is a big gap in time scale between, on the one hand, storms and floods and, on the other hand, topographic evolution. Many landscape evolution models have therefore used the “effective discharge” concept, or the idea that there is some value of discharge that represents the cumulative geomorphic effect of the natural sequence of storms and floods. Willgoose, Bras, and Rodriguez-Iturbe (1991) used mean peak discharge, but Huang and Niemann (2006) recognized that the return period of effective discharge events is not necessarily the same at different times and places.
Basically, landscape models tend to use one of four methods:
Steady flow with uniform precipitation or a specified runoff coefficient (effective discharge concept)
Steady flow with nonuniform precipitation or runoff (e.g., orographic precipitation)
Stochastic-in-time, spatially uniform runoff generation
“Short storms” model (Sólyom and Tucker 2004)
We will not examine all of these in detail. Instead, we will take a brief look at the Poisson rectangular pulse model implemented in CHILD.
Exercise 5: Visualizing a Poisson Storm Sequence
>> In WMT, open the model titled "Rainfall1." Save and submit the job.
>> Download the results and move them to the folder childFolderLocation∖ChildExercises∖rainfall1. For childFolderLocation, use the path to the Child visualization tools package that you downloaded.
>> In Matlab, navigate to the rainfall1 folder. Type:
- figure(1), clf, cstormplot( 'rainfall1' );
- figure(2), clf, cstormplot( 'rainfall1', 10 );
The first plot shows a 1-year simulated storm sequence; the second shows just the first 10 storms.
The motivation for using a stochastic flow model is (1) that nature is effectively stochastic, and (2) variability matters when the erosion or transport rate is a nonlinear function of flow. For more on this, see Tucker and Bras (2000); Snyder et al. (2003); Tucker (2004);, and DiBiase and Whipple (2011).
Remarks
Landscape evolution models can be, and have been, used to study climate impacts on erosion, topography, and mountain building. But be careful—climate and hydrology amount to much more than a “sprinkler over the landscape.”
Hydraulic Geometry
Channel size, shape, and roughness control delivery of hydraulic force to the bed and banks. Most landscape models either implicitly assume constant width (practical but dangerous) or use the empirical relation W = KwQb, where b ≈ 0. 5. Models with time-varying discharge must also specify how width varies at a point along the channel as Q rises and falls. Width-discharge scaling is practical but incomplete, because channels may narrow or widen downstream in concert with variations in incision rate, as observed in Italy (Whittaker et al. 2007), Nepal (Lavé and Avouac 2001), New Zealand (Amos and Burbank 2007), Taiwan (Yanites et al. 2010), and California (Duvall, Kirby, and Burbank 2004). Some models have begun to explore these sensitivities (Wobus, Tucker, and Anderson 2006; Wobus et al. 2008; Attal et al. 2008; Turowski, Lague, and Hovius 2009; Yanites and Tucker 2010), but full treatment of the channel geometry adjustment problem is a frontier area.
References
Ahnert, F. 1976. “Brief Description of a Comprehensive Three-Dimensional Process-Response Model of Landform Development.” Zeitschrift FÜR Geomorfologie, Supplementband 25: 29–49.
Ahnert, F. 1971. “Brief Description of a Comprehensive Three-Dimensional Process-Response Model of Landform Development.” Zeitschrift Fur Geomorfologie, Supplementband 25: 29–49.
Amos, Colin B, and Douglas W Burbank. 2007. “Channel Width Response to Differential Uplift.” Journal of Geophysical Research: Earth Surface (2003–2012) 112 (F2).
Attal, M., G. E. Tucker, A. C. Whittaker, P. A. Cowie, and G P Roberts. 2008. “Modeling Fluvial Incision and Transient Landscape Evolution: Influence of Dynamic Channel Adjustment.” Journal of Geophysical Research 113: F03013.
Beaumont, C., P. Fullsack, and J. Hamilton. 1992. “Erosional Control of Active Compressional Orogens.” Thrust Tectonics 99: 1–18.
Braun, Jean, and Malcom Sambridge. 1997. “Modelling Landscape Evolution on Geological Time Scales: a New Method Based on Irregular Spatial Discretization.” Basin Research 9: 27–52.
Carretier, S., and F. Lucazeau. 2005. “How Does Alluvial Sedimentation at Range Fronts Modify the Erosional Dynamics of Mountain Catchments?” Basin Research 17 (3): 361–381.
Chase, Clement G. 1992. “Fluvial Landsculpting and the Fractal Dimension of Topography.” Geomorphology 5: 39–57.
Clevis, Q., G. Tucker, S. Lancaster, A. Desitter, N. Gasparini, and G. Lock. 2006. “Geoarchaeological Simulation of Meandering River Deposits and Settlement Distributions: a Three-Dimensional Approach.” Computers and Geosciences 21 (8): 843–874.
Collins, DBG, RL Bras, and GE Tucker. 2004. “Modeling the Effects of Vegetation-Erosion Coupling on Landscape Evolution.” Journal of Geophysical Research—Earth Surface 109 (F3) ({AUG 3}). doi:10.1029/2003JF000028.
Coulthard, TJ, MJ Kirkby, and MG Macklin. 1996. “A Cellular Automaton Landscape Evolution Model.” Proceedings of the First International Conference on GeoComputation.
Crave, A, and Ph Davy. 2001. “A Stochastic ’Precipiton’ Model for Simulating Erosion/Sedimentation Dynamics.” Computers and Geosciences 27: 815–827.
Crosby, Benjamin T., Kelin X. Whipple, Nicole M. Gasparini, and Cameron W. Wobus. 2007. “Formation of Fluvial Hanging Valleys: Theory and Simulation.” JOURNAL OF GEOPHYSICAL RESEARCH-EARTH SURFACE 112 (F3) ({AUG 9}). doi:10.1029/2006JF000566.
Culling, WEH. 1963. “Soil Creep and the Development of Hillside Slopes.” The Journal of Geology: 127–161.
Densmore, Alexander L, Michael A Ellis, and Robert S Anderson. 1998. “Landsliding and the Evolution of Normal-Fault-Bounded Mountains.” Journal of Geophysical Research 103: 15203–15219.
DiBiase, R.A., and K.X. Whipple. 2011. “The Influence of Erosion Thresholds and Runoff Variability on the Relationships Among Topography, Climate, and Erosion Rate.” Journal of Geophysical Research 116 (F4): F04036.
Duvall, A., E. Kirby, and D. Burbank. 2004. “Tectonic and Lithologic Controls on Bedrock Channel Profiles and Processes in Coastal California.” Journal of Geophysical Research 109 (F3): F03002.
Fagherazzi, S., A.D. Howard, and P.L. Wiberg. 2002. “An Implicit Finite Difference Method for Drainage Basin Evolution.” Water Resources Research 38 (7): 21.
Flores-Cervantes, Homero, Erkan Istanbulluoglu, and Rafael L Bras. 2006. “Development of Gullies on the Landscape: a Model of Headcut Retreat Resulting from Plunge Pool Erosion.” Journal of Geophysical Research 111: F01010.
Garcia-Castellanos, D. 2002. “Interplay Between Lithospheric Flexure and River Transport in Foreland Basins.” Basin Research 14 (2): 89–104.
Gasparini, N., G. Tucker, and R. Bras. 1999. "Downstream fining through selective particle sorting in an equilibrium drainage network." Geology 27(12), 1079.
Gasparini, N., G. Tucker, and R. Bras. 2004. "Network-scale dynamics of grain-size sorting: Implications for downstream fining, stream-profile concavity, and drainage basin morphology. Earth Surface Processes and Landforms 29(4), 401-421.
Gasparini, N. M., K. X. Whipple, and R. L. Bras. 2007. “Predictions of Steady State and Transient Landscape Morphology Using Sediment-Flux-Dependent River Incision Models.” Journal of Geophysical Research Earth Surface 112 (F3) ({MAY 19}). doi: 10.1029/2006JF000567.
Gilbert, GK. 1877. “Report on the Geology of the Henry Mountains: US Geog. and Geol.” Survey, Rocky Mtn. Region 160.
Herman, F., and J. Braun. 2006. “Fluvial Response to Horizontal Shortening and Glaciations: a Study in the Southern Alps of New Zealand.” Journal of Geophysical Research-Earth Surface 111 (F1): F01008.
Herman, F., and J. Braun. 2008. “Evolution of the Glacial Landscape of the Southern Alps of New Zealand: Insights from a Glacial Erosion Model.” Journal of Geophysical Research-Earth Surface 113 (F2): F02009.
Herman, F., J. Braun, and W.J. Dunlap. 2007. “Tectonomorphic Scenarios in the Southern Alps of New Zealand.” Journal of Geophysical Research-Solid Earth 112 (B4): B04201.
Howard, A. 1971. “Simulation Model of Stream Capture.” Geological Society of America Bulletin 82 (5): 1355–1376.
Howard, Alan D. 1994. “A Detachment-Limited Model of Drainage Basin Evolution.” Water Resources Research 30 (7): 2261–2285.
Huang, X., and J.D. Niemann. 2006. “An Evaluation of the Geomorphically Effective Event for Fluvial Processes over Long Periods.” Journal of Geophysical Research 111 (F3): F03015.
Istanbulluoglu, Erkan, and Rafael L. Bras. 2005. “Vegetation-Modulated Landscape Evolution: Effects of Vegetation on Landscape Processes, Drainage Density, and Topography.” Journal of Geophysical Research 110: F02012.
Istanbulluoglu, Erkan, Rafael L. Bras, Homero Flores-Cervantes, and Gregory E. Tucker. 2005. “Implications of Bank Failures and Fluvial Erosion for Gully Development: Field Observations and Modeling.” Journal of Geophysical Research 110: F01014.
Kirkby, MJ. 1971. “Hillslope Process-Response Models Based on the Continuity Equation.” Inst. Br. Geogr. Spec. Publ 3: 15–30.
Lancaster, S.T., S.K. Hayes, and G.E. Grant. 2003. “Effects of Wood on Debris Flow Runout in Small Mountain Watersheds.” Water Resources Research 39 (6): 1168.
Lavé, J., and JP Avouac. 2001. “Fluvial Incision and Tectonic Uplift Across the Himalayas of Central Nepal.” Journal of Geophysical Research 106 (B11): 26561.
Mitas, L., and H. Mitasova. 1998. “Distributed Soil Erosion Simulation for Effective Erosion Prevention.” Water Resources Research 34 (3): 505–516.
Murray, A.B., and C. Paola. 1994. “A Cellular Model of Braided Rivers.” Nature 371 (6492): 54–57.
Perron, J.T. 2011. “Numerical Methods for Nonlinear Hillslope Transport Laws.” Journal of Geophysical Research 116 (F2): F02021.
Press, W.H., S.A. Teukolsky, W.T. Vetterling, and B.P. Flannery. 2007. Numerical Recipes: the Art of Scientific Computing. Cambridge Univ Pr.
Schoorl, JM, A. Veldkamp, and J. Bouma. 2002. “Modeling Water and Soil Redistribution in a Dynamic Landscape Context.” Soil Science Society of America Journal 66 (5): 1610.
Snyder, N.P., K.X. Whipple, G.E. Tucker, and D.J. Merritts. 2003. “Importance of a Stochastic Distribution of Floods and Erosion Thresholds in the Bedrock River Incision Problem.” Journal of Geophysical Research 108 (B2): 2117.
Sólyom, P.B., and G.E. Tucker. 2004. “Effect of Limited Storm Duration on Landscape Evolution, Drainage Basin Geometry, and Hydrograph Shapes.” Journal of Geophysical Research 109: 13.
Tucker, G E, and R L Slingerland. 1994. “Erosional Dynamics, Flexural Isostasy, and Long-Lived Escarpments: a Numerical Modeling Study.” Journal of Geophysical Research 99: 12, 229–12, 243.
Tucker, GE. 2004. “Drainage Basin Sensitivity to Tectonic and Climatic Forcing: Implications of a Stochastic Model for the Role of Entrainment and Erosion Thresholds.” Earth Surface Processes and Landforms 29 (2) ({FEB}): 185–205. doi:10.1002/esp.1020.
Tucker, Gregory E, and Rafael L Bras. 2000. “A Stochastic Approach to Modeling the Role of Rainfall Variability in Drainage Basin Evolution.” Water Resources Research 36 (7): 1953–1964.
Tucker, Gregory E, and Gregory R Hancock. 2010. “Modelling Landscape Evolution.” Earth Surface Processes and Landforms 46: 28–50.
Tucker, Gregory E, S T Lancaster, Nicole M Gasparini, and Rafael L Bras. 2001. “The Channel-Hillslope Integrated Landscape Development Model (CHILD).” In Landscape Erosion and Evolution Modeling, edited by R. S. Harmon and W. W. Doe, 349–388. Dordrecht: Kluwer Press.
Tucker, Gregory E, S T Lancaster, Nicole M Gasparini, Rafael L Bras, and S M Rybarczyk. 2001. “An Object-Oriented Framework for Hydrologic and Geomorphic Modeling Using Triangular Irregular Networks.” Computers and Geosciences 27: 959–973.
Turowski, Jens M, Dimitri Lague, and Niels Hovius. 2009. “Response of Bedrock Channel Width to Tectonic Forcing: Insights from a Numerical Model, Theoretical Considerations, and Comparison with Field Data.” Journal of Geophysical Research: Earth Surface (2003–2012) 114 (F3).
Whipple, K X, and G E Tucker. 1999. “Dynamics of the Stream-Power River Incision Model: Implications for Height Limits of Mountain Ranges, Landscape Response Timescales, and Research Needs.” Journal of Geophysical Research 104: 17661–17674.
Whipple, K. X., and G. E. Tucker. 2002. “Implications of Sediment-Flux-Dependent River Incision Models for Landscape Evolution.” Journal of Geophysical Research 107.
Whittaker, A.C., P.A. Cowie, M. Attal, G.E. Tucker, and G.P. Roberts. 2007. “Bedrock Channel Adjustment to Tectonic Forcing: Implications for Predicting River Incision Rates.” Geology 35 (2): 103.
Willgoose, Garry, Rafael L Bras, and Ignacio Rodriguez-Iturbe. 1991. “A Coupled Channel Network Growth and Hillslope Evolution Model, 1, Theory.” Water Resources Research 27 (7): 1671–1684.
Wobus, C.W., J.W. Kean, G.E. Tucker, and R.S. Anderson. 2008. “Modeling the Evolution of Channel Shape: Balancing Computational Efficiency with Hydraulic Fidelity.” Journal of Geophysical Research 113.
Wobus, C.W., G.E. Tucker, and R.S. Anderson. 2006. “Self-Formed Bedrock Channels.” Geophys. Res. Lett 33: 1–6.
Yanites, B.J., and G.E. Tucker. 2010. “Controls and Limits on Bedrock Channel Geometry.” Journal of Geophysical Research 115 (F4): F04019.
Yanites, B.J., G.E. Tucker, K.J. Mueller, Y.G. Chen, T. Wilcox, S.Y. Huang, and K.W. Shi. 2010. “Incision and Channel Morphology Across Active Structures Along the Peikang River, Central Taiwan: Implications for the Importance of Channel Width.” Geological Society of America Bulletin 122 (7-8): 1192.