Labs Landscape Evolution Modeling With Child Part 1
Landscape Evolution Modeling with CHILD
Part 1: Overview, Introduction, Continuity of Mass and Discretization, and Gravitational Hillslope Transport
Gregory E. Tucker, University of Colorado Boulder, and Stephen T. Lancaster, Oregon State University
If you have never used the Web Modeling Tool, learn how to use it here. You will need an account on the CSDMS supercomputer to submit your jobs.
More information on getting an account can be found here Beach HPCC Access
Before beginning these exercises, please download the CHILD visualization tools here: File:CHILDVisTools.tar.gz.
Overview
The learning goals of these exercises are:
- To appreciate that working with landscape Evolution Models, LEMs, involves choosing a level of simplification in the governing physics that is appropriate to the problem at hand.
- To get a sense for how and why soil creep produces convex hillslopes.
- To appreciate the concepts of transient versus steady topography.
- To acquire a feel for the similarity and difference between detachment-limited and transport-limited modes of fluvial erosion.
- To understand the connection between fluvial physics and slope-area plots.
- To appreciate that LEMs (1) are able to reproduce (and therefore, at least potentially, explain) common forms in fluvially carved landscapes, (2) can enhance our insight into dynamics via visualization and experimentation, but (3) leave open many important questions regarding long-term process physics.
- To develop a sense of “best practices” in using landscape evolution models.
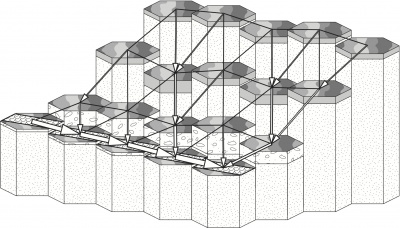
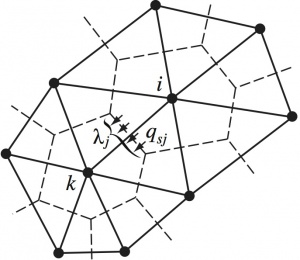
Fig. 1: Schematic diagram of CHILD model's representation of the landscape: hexagonal Voronoi cells, nodes (at centers of cells) connected by the edges of the Delaunay triangulation, vegetated cell surfaces, channelized cells, and soil and sediment layers above bedrock.
Introduction to LEMs
Brief History
G.K. Gilbert, a member of the Powell Expedition, produced “word pictures” of landscape evolution that still provide insight. For example, consider his “Law of Divides” (Gilbert 1877):
- We have seen that the declivity over which water flows bears an inverse relation to the quantity of water. If we follow a stream from its mouth upward and pass successively the mouths of its tributaries, we find its volume gradually less and less and its grade steeper and steeper, until finally at its head we reach the steepest grade of all. If we draw the profile of the river on paper, we produce a curve concave upward and with the greatest curvature at the upper end. The same law applies to every tributary and even to the slopes over which the freshly fallen rain flows in a sheet before it is gathered into rills. The nearer the water-shed or divide the steeper the slope; the farther away the less the slope.
- It is in accordance with this law that mountains are steepest at their crests. The profile of a mountain if taken along drainage lines is concave outward...; and this is purely a matter of sculpture, the uplifts from which mountains are carved rarely if ever assuming this form.
Flash forward to the 1960’s, and we find the emergence of the first one-dimensional profile models. Culling (1963), for example, used the diffusion equation to describe the relaxation of escarpments over time.
Models became more sophisticated in the early 1970’s. Frank Ahnert and Mike Kirkby, among others, began to develop computer models of slope profile development and included not only diffusive soil creep but also fluvial downcutting as well as weathering (Ahnert 1971; Kirkby 1971). Meanwhile, Alan Howard developed a simulation model of channel network evolution (Howard 1971).
The mid-1970’s saw the first emergence of fully two-dimensional (and even quasi-three-dimensional) landscape evolution models, perhaps most noteworthy that of Ahnert (1976). Geomorphologists would have to wait nearly 15 years for models to surpass the level of sophistication found in this early model.
During that time, computers would become much more powerful and able to model full landscapes. The late 1980’s through the mid-1990’s saw the beginning of the “modern era” of landscape evolution models, and today there are many model codes with as many applications, scales, and objectives, ranging from soil erosion to continental collision (Table 1).
Brief Overview of Models and their Uses
Some examples of landscape evolution models (LEMs) are shown in Table 1. LEMs have been developed to represent, for example, coupled erosion-deposition systems, meandering, Mars cratering, forecasting of mine-spoil degradation, and estimation of erosion risk to buried hazardous waste. These models provide powerful tools, but their process ingredients are generally provisional and subject to testing. For this reason, it is important to have continuing cross-talk between modeling and observations—after all, that’s how science works.
In this exercise, we provide an overview of how a LEM works, including how terrain and water flow are represented numerically, and how various processes are computed.
| Model | Example reference | Notes |
|---|---|---|
| SIBERIA | Willgoose, Bras, and Rodriguez-Iturbe (1991) | Transport-limited; |
| Channel activator function | ||
| DRAINAL | Beaumont, Fullsack, and Hamilton (1992) | “Undercapacity” concept |
| GILBERT | Chase (1992) | Precipiton |
| DELIM/MARSSIM | Howard (1994) | Detachment-limited; |
| Nonlinear diffusion | ||
| GOLEM | Tucker and Slingerland (1994) | Regolith generation; |
| Threshold landsliding | ||
| CASCADE | Braun and Sambridge (1997) | Irregular discretization |
| CAESAR | Coulthard, Kirkby, and Macklin (1996) | Cellular automaton algorithm |
| for 2D flow field | ||
| ZSCAPE | Densmore, Ellis, and Anderson (1998) | Stochastic bedrock |
| landsliding algorithm | ||
| CHILD | Tucker and Bras (2000) | Stochastic rainfall |
| EROS | Crave and Davy (2001) | Modified precipiton |
| TISC | Garcia-Castellanos (2002) | Thrust stacking |
| LAPSUS | Schoorl, Veldkamp, and Bouma (2002) | Multiple flow directions |
| APERO/CIDRE | Carretier and Lucazeau (2005) | Single or multiple |
| flow directions |
Table 1: Partial list of numerical landscape models published between 1991 and 2005.
Continuity of Mass and Discretization
A typical mass continuity equation for a column of soil or rock is:
where η is the elevation of the land surface [L]; t is time; B [L/T] represents the vertical motion of the rocks and soil relative to baselevel (due, for example, to tectonic uplift or subsidence, sea-level change, or erosion along the boundary of the system); and q⃗s is sediment flux per unit width [L2/T]. (The letters in square brackets indicate the dimensions of each variable; L stands for length, T for time, and M for mass.) This is one of several variations; for discussion of others, see Tucker and Hancock (2010). Some models, for example, distinguish between a regolith layer and the bedrock underneath (Fig. 1). Note that this type of mass continuity equation applies only to terrain that has one and only one surface point for each coordinate; it would not apply to a vertical cliff or an overhang.
A LEM computes η(x, y, t) given (1) a set of process rules, (2) initial conditions, and (3) boundary conditions. One thing all LEMs have in common is that they divide the terrain into discrete elements. Often these are square elements, but sometimes they are irregular polygons (as in the case of CASCADE and CHILD; Fig. 1). For a discrete parcel (or “cell”) of land, continuity of mass enforced by the following equation (in words):
Time rate of change of mass in element = mass rate in at boundaries - mass rate out at boundaries + inputs or outputs from above or below (tectonics, dust deposition, etc.)
This statement can be expressed mathematically, for cell i, as follows:
where Λ i is the horizontal surface area of cell i; N is the number of faces surrounding cell i; qsj is the unit flux across face j; and λj is the length of face j (Fig. 2). (Note that, for the sake of simplicity, we are using volume rather than mass flux; this is ok as long as the mass density of the material is unchanging). Equation (2) expresses what is known as a finite-volume method because it is based on computing fluxes in and out along the boundaries of a finite volume of space.
Some terminology: a cell is a patch of ground with boundaries called faces. A node is the point inside a cell at which we track elevation (and other properties). On a raster grid, each cell is square and each node lies at the center of a cell. On the irregular mesh used by CASCADE and CHILD, the cell is the area of land that is closer to that particular node than to any other node in the mesh. (It is a mathematical entity known as a Voronoi cell or Thiessen polygon; for more, see Braun and Sambridge (1997), Gregory E Tucker, Lancaster, Gasparini, Bras, et al. (2001).)
Equation (2) gives us the time derivatives for the elevation of every node on the grid. How do we solve for the new elevations at time t? There are many ways to do this, including matrix-based implicit solvers (see for example Fagherazzi, Howard, and Wiberg (2002); Perron (2011)). We won’t get into the details of numerical solutions (at least not yet), but for now note that the simplest solution is the forward-difference approximation:
The main disadvantage of this approach is that very small time steps are typically needed in order to ensure numerical stability. (CHILD uses a variant of this that seeks the largest possible stable value of Δ t at each iteration). A good discussion of numerical stability, accuracy, and alternative methods for diffusion-like problems can be found in Press et al. (2007).
Gravitational Hillslope Transport
Geomorphologists often distinguish between hillslope and channel processes. It’s a useful distinction, although one has to bear in mind that the transition is not always abrupt, and even where it is abrupt, it is commonly either discontinuous or highly dynamic or both.
Alternatively, one can also distinguish between processes that are driven nearly exclusively by gravitational processes, and those that involve a fluid phase (normally water or ice). This distinction too has a gray zone: landslides are gravitational phenomena but often triggered by fluid pore pressure, while debris flows are surges of mixed fluid and solid. Nonetheless, we will start with a consideration of one form of gravitational transport on hillslopes: soil creep.
Linear Diffusion
For relatively gentle, soil-mantled slopes, there is reasonably strong support for a transport law of the form:
where D is a transport coefficient with dimensions of L2T − 1. Using the finite-volume method outlined in Equation (2), we want to calculate $\vec{q_s}$ at each of the cell faces. Suppose node i and node k are neighboring nodes that share a common face (we’ll call this face j). We approximate the gradient between nodes i and k as:
where Lik is the distance between nodes. On a raster grid, Lik = Δ x is simply the grid spacing. The sediment flux per unit width is then
where qsik is the volume flux per unit width from node k to node i (if negative, sediment flows from i to k), and Lik is the distance between nodes. To compute the total sediment flux through face j, we simply multiply the unit flux by the width of face j, which we denote λij (read as “the j-th face of cell i”):
Exercise 1: Getting Set Up with CHILD
Our first exercise is simply to ensure that everything is in place for CHILD to be run and visualized. Note that Matlab is required to run the visualization scripts. You should already have an account on WMT and an account on beach. Note that your login credentials may not be the same for WMT as for beach.
>> If you do not have an account on beach, request one here.
>> If you do not have an account on WMT, create one here.
>> If you have not downloaded the visualization tools, download them here: File:CHILDVisTools.tar.gz.
>>On a PC you can use 7zip (a free download in case it does not come installed with your system). You will have to run the unpacking two times, once to get rid of the gz, once to untar.
>> Move the visualization tools from the download folder to an easy-to-find location such as the Desktop and extract the files by opening a terminal, navigating to the folder location, and typing:
tar -zxvf CHILDVisTools.tar.gz
>> Note that your browser might partially extract the files for you. In that case, you may only need to type:
tar -xvf CHILDVisTools.tar
Let’s get ready to visualize the output. Start Matlab. The first thing we will do is tell Matlab where to look for the plotting programs that we will use.
>>At the Matlab command prompt type: path( path, ’childFolderLocation∖ChildExercises∖MatlabScripts’ ) For childFolderLocation, use the path name of the folder that contains the unzipped visualization scripts. You can also add a folder to your path by selecting File-Set Path... from the menu.
Note that the “package” also includes some documentation that you may find useful: the ChildExercises folder contains an earlier version of this document, and the Doc folder contains the Users’ Guide (child_users_guide.pdf). The guide covers the nuts and bolts of the model in much greater detail than these exercises and includes a full list of input parameters. Finally, there is an "Output" folder with several empty subfolders; we will use these folders later to hold the outputs of our model runs.
Exercise 2: Hillslope Diffusion and Parabolic Slopes with CHILD
>> In a web browser, go to https://csdms.colorado.edu/wmt/.
>> Log in with your email address and password.
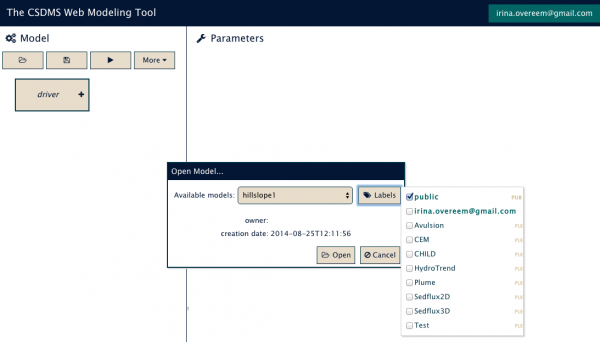
>> Click the "open folder" icon.
>> Click the button marked "Labels."
>> Check the box labeled "public"
>> From the drop-down menu, select "hillslope1" and click "open."
>> You will have to save the model first to your own personal copy. Click the "save as" button under "more" tab
>> Enter your beach username and password to submit the model. Note that your beach username and password are the same as your IdentiKey username and password, which may not be the same as your WMT information.
>> Click "view run status" to be taken to the results download page. This will open a new tab.
>> This run should take about 30 seconds on WMT. After 30 seconds, refresh the page and download the results by clicking the download button.
>> Navigate to your browser's download folder and untar the model results. Move all of the output files to the folder childFolderLocation∖ChildExercises∖hillslope1 . For childFolderLocation, use the path to the Child visualization tools package that you downloaded.
>> Return to Matlab and type:
cd('childFolderLocation/hillslope1')
For childFolderLocation, use the path name of the folder that contains the unzipped visualization scripts.
m = cmovie( 'hillslope1', 21, 200, 200, 100, 50 );
This command says ``generate a 21-frame movie from the run `hillslope1' with the x-, y- and z- axes set to 200, 200 and 100 m, respectively, and with the color range representing 0 to 50 m elevation.
To replay the movie, type:
movie
(Windows note: we found that under Vista and Windows 7, the movie figure gets erased after display; slightly re-sizing the figure window seems to fix this).
The analytical solution to elevation as a function of cross-ridge distance y is:
where L is the half-width of the ridge (100 m in this case) and y0 is the position of the ridge crest (also 100 m). The effective uplift rate U, represented in the input file by the parameter UPRATE, is 10-4 m/yr. The diffusivity coefficient D, represented in the input file by parameter KD, is 0.01 m2/yr. You can view these parameters in the input file generated by WMT by navigating to childFolderLocation∖ChildExercises∖hillslope1 and using a text editor to open the file child.in.
Next, we'll make a plot that compares the computed and analytical solutions.
>> Enter the following in Matlab:
- cd('childFolderLocation∖ChildExercises∖hillslope1') \% For childFolderLocation, use the location of the child visualization packet that you downloaded
- ya = 0:200; \% This is our x-coordinate
- U = 0.0001; D = 0.01; y0 = 100; L = 100;
- za = ((U/(2*D))*((L^2)-((ya-y0)).^2));
- figure(2), plot( ya, za ), hold on
- xyz = creadxyz( 'hillslope1', 21 ); \% Reads node coords, time 21
- plot( xyz(:,2), xyz(:,3), 'r.' ), hold off
- legend( 'Analytical solution', 'CHILD Nodes'
Diffusion theory predicts that equilibrium height varies linearly with U, inversely with D, and as the square of L.
>> In WMT, change one of these three parameters. To change U, edit the number in the box labeled "duration of uplift (yr)". Similarly, to change D, edit the value of the diffusivity coefficient, parameter KD. If you want to try a different ridge width L, change "Length of grid in x-direction," "Length of grid in y-direction," and "Grid spacing" by the same proportion (changing the grid spacing} will ensure that you keep the same number of model nodes).
>> Re-run CHILD with your modified input file and see what happens. Create a second folder to hold the new model output if you would like to compare the two simulations side-by-side.
Nonlinear Diffusion
As we found in our study of hillslope transport processes, the simple slope-linear transport law works poorly for slopes that are not ``small" relative to the angle of repose for sediment and rock. The next example explores what happens to our ridge when we (1) increase the relative uplift rate, and (2) use the nonlinear diffusion transport law:
Exercise 3: Nonlinear Diffusion and Planar Slopes
>> Open the "hillslope2" model in WMT. Save and submit the job.
>> When the 70,000-year run finishes, download the results and move them to the folder childFolderLocation∖ChildExercises∖hillslope2. For childFolderLocation, use the path to the Child visualization tools package that you downloaded.
>> In Matlab, navigate to the hillslope2 folder:
cd('childFolderLocation∖ChildExercises∖hillslope2')
>> Type in Matlab:
m = cmovie( 'hillslope2', 21, 200, 200, 100, 70 );
If we had used linear diffusion, the equilibrium slope gradient along the edges of the ridge would be = UL/D = (0.001)(100)/(0.01) = 10 m/m, or about 84<math>^\circ</math>! Instead, the actual computed gradient is close to the threshold limit of 0.7. Notice too how the model solution speed slowed down. This reflects the need for especially small time steps when the slopes are close to the threshold angle.
Remarks
There is a lot more to mass movement than what is encoded in these simple diffusion-like transport laws. Some models include stochastic landsliding algorithms (e.g., CASCADE, ZSCAPE). Some impose threshold slopes (e.g., GOLEM). One spinoff version of CHILD even includes debris-flow generation and routing (Lancaster, Hayes, and Grant 2003).
References
- Ahnert, F. 1976. “Brief Description of a Comprehensive Three-Dimensional Process-Response Model of Landform Development.” Zeitschrift FÜR Geomorfologie, Supplementband 25: 29–49.
- Ahnert, F. 1971. “Brief Description of a Comprehensive Three-Dimensional Process-Response Model of Landform Development.” Zeitschrift Fur Geomorfologie, Supplementband 25: 29–49.
- Amos, Colin B, and Douglas W Burbank. 2007. “Channel Width Response to Differential Uplift.” Journal of Geophysical Research: Earth Surface (2003–2012) 112 (F2).
- Attal, M., G. E. Tucker, A. C. Whittaker, P. A. Cowie, and G P Roberts. 2008. “Modeling Fluvial Incision and Transient Landscape Evolution: Influence of Dynamic Channel Adjustment.” Journal of Geophysical Research 113: F03013.
- Beaumont, C., P. Fullsack, and J. Hamilton. 1992. “Erosional Control of Active Compressional Orogens.” Thrust Tectonics 99: 1–18.
- Braun, Jean, and Malcom Sambridge. 1997. “Modelling Landscape Evolution on Geological Time Scales: a New Method Based on Irregular Spatial Discretization.” Basin Research 9: 27–52.
- Carretier, S., and F. Lucazeau. 2005. “How Does Alluvial Sedimentation at Range Fronts Modify the Erosional Dynamics of Mountain Catchments?” Basin Research 17 (3): 361–381.
- Chase, Clement G. 1992. “Fluvial Landsculpting and the Fractal Dimension of Topography.” Geomorphology 5: 39–57.
- Clevis, Q., G. Tucker, S. Lancaster, A. Desitter, N. Gasparini, and G. Lock. 2006. “Geoarchaeological Simulation of Meandering River Deposits and Settlement Distributions: a Three-Dimensional Approach.” Computers and Geosciences 21 (8): 843–874.
- Collins, DBG, RL Bras, and GE Tucker. 2004. “Modeling the Effects of Vegetation-Erosion Coupling on Landscape Evolution.” Journal of Geophysical Research—Earth Surface 109 (F3) ({AUG 3}). doi:10.1029/2003JF000028.
- Coulthard, TJ, MJ Kirkby, and MG Macklin. 1996. “A Cellular Automaton Landscape Evolution Model.” Proceedings of the First International Conference on GeoComputation.
- Crave, A, and Ph Davy. 2001. “A Stochastic ’Precipiton’ Model for Simulating Erosion/Sedimentation Dynamics.” Computers and Geosciences 27: 815–827.
- Crosby, Benjamin T., Kelin X. Whipple, Nicole M. Gasparini, and Cameron W. Wobus. 2007. “Formation of Fluvial Hanging Valleys: Theory and Simulation.” JOURNAL OF GEOPHYSICAL RESEARCH-EARTH SURFACE112 (F3) ({AUG 9}). doi:10.1029/2006JF000566.
- Culling, WEH. 1963. “Soil Creep and the Development of Hillside Slopes.” The Journal of Geology: 127–161.
- Densmore, Alexander L, Michael A Ellis, and Robert S Anderson. 1998. “Landsliding and the Evolution of Normal-Fault-Bounded Mountains.” Journal of Geophysical Research 103: 15203–15219.
- DiBiase, R.A., and K.X. Whipple. 2011. “The Influence of Erosion Thresholds and Runoff Variability on the Relationships Among Topography, Climate, and Erosion Rate.” Journal of Geophysical Research 116 (F4): F04036.
- Duvall, A., E. Kirby, and D. Burbank. 2004. “Tectonic and Lithologic Controls on Bedrock Channel Profiles and Processes in Coastal California.” Journal of Geophysical Research 109 (F3): F03002.
- Fagherazzi, S., A.D. Howard, and P.L. Wiberg. 2002. “An Implicit Finite Difference Method for Drainage Basin Evolution.” Water Resources Research 38 (7): 21.
- Flores-Cervantes, Homero, Erkan Istanbulluoglu, and Rafael L Bras. 2006. “Development of Gullies on the Landscape: a Model of Headcut Retreat Resulting from Plunge Pool Erosion.” Journal of Geophysical Research 111: F01010.
- Garcia-Castellanos, D. 2002. “Interplay Between Lithospheric Flexure and River Transport in Foreland Basins.” Basin Research 14 (2): 89–104.
- Gasparini, N., G. Tucker, and R. Bras. 1999. "Downstream fining through selective particle sorting in an equilibrium drainage network." Geology 27(12), 1079.
- Gasparini, N., G. Tucker, and R. Bras. 2004. "Network-scale dynamics of grain-size sorting: Implications for downstream fining, stream-profile concavity, and drainage basin morphology. Earth Surface Processes and Landforms 29(4), 401-421.
- Gasparini, N. M., K. X. Whipple, and R. L. Bras. 2007. “Predictions of Steady State and Transient Landscape Morphology Using Sediment-Flux-Dependent River Incision Models.” Journal of Geophysical Research Earth Surface 112 (F3) ({MAY 19}). doi: 10.1029/2006JF000567.
- Gilbert, GK. 1877. “Report on the Geology of the Henry Mountains: US Geog. and Geol.” Survey, Rocky Mtn. Region 160.
- Herman, F., and J. Braun. 2006. “Fluvial Response to Horizontal Shortening and Glaciations: a Study in the Southern Alps of New Zealand.” Journal of Geophysical Research-Earth Surface 111 (F1): F01008.
- Herman, F., and J. Braun. 2008. “Evolution of the Glacial Landscape of the Southern Alps of New Zealand: Insights from a Glacial Erosion Model.” Journal of Geophysical Research-Earth Surface 113 (F2): F02009.
- Herman, F., J. Braun, and W.J. Dunlap. 2007. “Tectonomorphic Scenarios in the Southern Alps of New Zealand.” Journal of Geophysical Research-Solid Earth 112 (B4): B04201.
- Howard, A. 1971. “Simulation Model of Stream Capture.” Geological Society of America Bulletin 82 (5): 1355–1376.
- Howard, Alan D. 1994. “A Detachment-Limited Model of Drainage Basin Evolution.” Water Resources Research 30 (7): 2261–2285.
- Huang, X., and J.D. Niemann. 2006. “An Evaluation of the Geomorphically Effective Event for Fluvial Processes over Long Periods.” Journal of Geophysical Research 111 (F3): F03015.
- Istanbulluoglu, Erkan, and Rafael L. Bras. 2005. “Vegetation-Modulated Landscape Evolution: Effects of Vegetation on Landscape Processes, Drainage Density, and Topography.” Journal of Geophysical Research 110: F02012.
- Istanbulluoglu, Erkan, Rafael L. Bras, Homero Flores-Cervantes, and Gregory E. Tucker. 2005. “Implications of Bank Failures and Fluvial Erosion for Gully Development: Field Observations and Modeling.” Journal of Geophysical Research 110: F01014.
- Kirkby, MJ. 1971. “Hillslope Process-Response Models Based on the Continuity Equation.” Inst. Br. Geogr. Spec. Publ 3: 15–30.
- Lancaster, S.T., S.K. Hayes, and G.E. Grant. 2003. “Effects of Wood on Debris Flow Runout in Small Mountain Watersheds.” Water Resources Research 39 (6): 1168.
- Lavé, J., and JP Avouac. 2001. “Fluvial Incision and Tectonic Uplift Across the Himalayas of Central Nepal.” Journal of Geophysical Research 106 (B11): 26561.
- Mitas, L., and H. Mitasova. 1998. “Distributed Soil Erosion Simulation for Effective Erosion Prevention.” Water Resources Research 34 (3): 505–516.
- Murray, A.B., and C. Paola. 1994. “A Cellular Model of Braided Rivers.” Nature 371 (6492): 54–57.
- Perron, J.T. 2011. “Numerical Methods for Nonlinear Hillslope Transport Laws.” Journal of Geophysical Research 116 (F2): F02021.
- Press, W.H., S.A. Teukolsky, W.T. Vetterling, and B.P. Flannery. 2007. Numerical Recipes: the Art of Scientific Computing. Cambridge Univ Pr.
- Schoorl, JM, A. Veldkamp, and J. Bouma. 2002. “Modeling Water and Soil Redistribution in a Dynamic Landscape Context.” Soil Science Society of America Journal 66 (5): 1610.
- Snyder, N.P., K.X. Whipple, G.E. Tucker, and D.J. Merritts. 2003. “Importance of a Stochastic Distribution of Floods and Erosion Thresholds in the Bedrock River Incision Problem.” Journal of Geophysical Research 108 (B2): 2117.
- Sólyom, P.B., and G.E. Tucker. 2004. “Effect of Limited Storm Duration on Landscape Evolution, Drainage Basin Geometry, and Hydrograph Shapes.” Journal of Geophysical Research 109: 13.
- Tucker, G E, and R L Slingerland. 1994. “Erosional Dynamics, Flexural Isostasy, and Long-Lived Escarpments: a Numerical Modeling Study.” Journal of Geophysical Research 99: 12, 229–12, 243.
- Tucker, GE. 2004. “Drainage Basin Sensitivity to Tectonic and Climatic Forcing: Implications of a Stochastic Model for the Role of Entrainment and Erosion Thresholds.” Earth Surface Processes and Landforms 29 (2) ({FEB}): 185–205. doi:10.1002/esp.1020.
- Tucker, Gregory E, and Rafael L Bras. 2000. “A Stochastic Approach to Modeling the Role of Rainfall Variability in Drainage Basin Evolution.” Water Resources Research 36 (7): 1953–1964.
- Tucker, Gregory E, and Gregory R Hancock. 2010. “Modelling Landscape Evolution.” Earth Surface Processes and Landforms 46: 28–50.
- Tucker, Gregory E, S T Lancaster, Nicole M Gasparini, and Rafael L Bras. 2001. “The Channel-Hillslope Integrated Landscape Development Model (CHILD).” In Landscape Erosion and Evolution Modeling, edited by R. S. Harmon and W. W. Doe, 349–388. Dordrecht: Kluwer Press.
- Tucker, Gregory E, S T Lancaster, Nicole M Gasparini, Rafael L Bras, and S M Rybarczyk. 2001. “An Object-Oriented Framework for Hydrologic and Geomorphic Modeling Using Triangular Irregular Networks.” Computers and Geosciences 27: 959–973.
- Turowski, Jens M, Dimitri Lague, and Niels Hovius. 2009. “Response of Bedrock Channel Width to Tectonic Forcing: Insights from a Numerical Model, Theoretical Considerations, and Comparison with Field Data.” Journal of Geophysical Research: Earth Surface (2003–2012) 114 (F3).
- Whipple, K X, and G E Tucker. 1999. “Dynamics of the Stream-Power River Incision Model: Implications for Height Limits of Mountain Ranges, Landscape Response Timescales, and Research Needs.” Journal of Geophysical Research 104: 17661–17674.
- Whipple, K. X., and G. E. Tucker. 2002. “Implications of Sediment-Flux-Dependent River Incision Models for Landscape Evolution.” Journal of Geophysical Research107.
- Whittaker, A.C., P.A. Cowie, M. Attal, G.E. Tucker, and G.P. Roberts. 2007. “Bedrock Channel Adjustment to Tectonic Forcing: Implications for Predicting River Incision Rates.” Geology 35 (2): 103.
- Willgoose, Garry, Rafael L Bras, and Ignacio Rodriguez-Iturbe. 1991. “A Coupled Channel Network Growth and Hillslope Evolution Model, 1, Theory.” Water Resources Research 27 (7): 1671–1684.
- Wobus, C.W., J.W. Kean, G.E. Tucker, and R.S. Anderson. 2008. “Modeling the Evolution of Channel Shape: Balancing Computational Efficiency with Hydraulic Fidelity.” Journal of Geophysical Research 113.
- Wobus, C.W., G.E. Tucker, and R.S. Anderson. 2006. “Self-Formed Bedrock Channels.” Geophys. Res. Lett 33: 1–6.
- Yanites, B.J., and G.E. Tucker. 2010. “Controls and Limits on Bedrock Channel Geometry.” Journal of Geophysical Research 115 (F4): F04019.
- Yanites, B.J., G.E. Tucker, K.J. Mueller, Y.G. Chen, T. Wilcox, S.Y. Huang, and K.W. Shi. 2010. “Incision and Channel Morphology Across Active Structures Along the Peikang River, Central Taiwan: Implications for the Importance of Channel Width.” Geological Society of America Bulletin 122 (7-8): 1192.