CSDMS 2011 annual meeting poster Mohamad Nasr-Azadani
TURBINS: A computational tool for three-dimensional, high-resolution simulations of particle-laden flows
Eckart Meiburg, UC Santa Barbara Santa Barbara California, United States. meiburg@engineering.ucsb.edu
Abstract:
An accurate, three-dimensional Navier–Stokes based immersed boundary code called TURBINS has been developed, validated and tested, for the purpose of simulating density-driven gravity and turbidity currents propagating over complex topographies. The code is second order accurate in space and third order in time, uses MPI, and employs a domain decomposition approach for parallelism. It makes use of multigrid preconditioners and Krylov iterative solvers for the systems of linear equations obtained by the finite difference discretization of the governing equations. Various boundary conditions on the complex geometry are imposed via the direct forcing variant of the immersed boundary approach, utilizing a stable interpolation method. Bi- and trilinear interpolations are employed in such a way that the original discretization accuracy is retained with no additional restriction on the time step. Weak and strong scaling tests were performed for a uniform flow over array of spheres. We obtain very good scaling results as expected for multigrid solvers. We perform convergence tests via uniform flow over cylinder. Both skin friction and pressure coefficients show very good agreement with results reported by other authors.
Subsequently, a computational investigation was conducted of mono-, bi- and polydisperse lock-exchange turbidity currents interacting with complex bottom topography. Our simulation results are compared against laboratory experiments of other authors. Several features of the flow such as deposit profiles, front location, suspended mass and runout length are discussed. For a monodisperse lock-exchange current propagating over a flat surface, we investigate the influence of the boundary conditions at the streamwise and top boundaries, and we generally find good agreement with corresponding laboratory experiments. However, we note some differences with a second set of experimental data for polydisperse turbidity currents over flat surfaces. A comparison with experimental data for bidisperse currents with varying mass fractions of coarse and fine particles yields good agreement for all cases except those where the current consists almost exclusively of fine particles. For polydisperse currents over a two-dimensional bottom topography, significant discrepancies are observed. Potential reasons are discussed, including erosion and bedload transport.
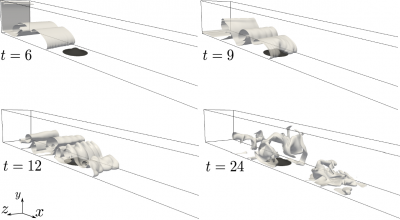
Finally, we investigate the influence of a three-dimensional Gaussian bump on the deposit pattern of a bidisperse current. The suspension includes two particle sizes with a settling velocity ratio of 10. As the current travels over the bottom topography, we record instantaneous deposit profiles and wall shear stress contours. As the current impinges on the obstacle, it becomes strongly three-dimensional (see Fig. 1). Comparison of the final deposit profiles near the Gaussian bump against the case of a flat surface shows a smaller influence of the topography on the fine particles than on the coarse ones. Due to lateral deflection, deposition generally decreases near the bump, while increasing away from it. Some distance downstream of the obstacle, the deposit profiles lose their memory of the bump and become nearly uniform again. Instantaneous wall shear stress profiles are employed in order to estimate the critical conditions at which bedload transport and/or particle resuspension can occur in various regions.
|
| CSDMS meeting abstract figure caption=Time evolution of the c = 0.1 concentration isosurface for a lock-exchange turbidity current interacting with a Gaussian bump for Re = 2,000. The suspension contains a mixture of two particle sizes, with nondimensional settling velocities equal to u_c = 0.035 and u_f = 0.0035$, and initial mass fractions of 90% and 10%, respectively. |
* Please acknowledge the original contributors when you are using this material. If there are any copyright issues, please let us know and we will respond as soon as possible.
