Mooring Dynamics and Design

Documentation on the "Dynamics Solution"
Richard K. Dewey, Centre for Earth and Ocean Research
University of Victoria, BC, Canada (250)-472-4009
RDewey@uvic.ca

The MATLAB set of routines to design and evaluate the dynamics of oceanographic moorings under the influence of 3 dimensional currents, solves a simple set of equations in order to determine the spatial position of each mooring element relative to the anchor. Although a matrix solution is possible, the present approach is both simple to code and interpret. Once a mooring has been constructed using the MORRDESIGN.M set of programs, the position of each mooring element within a 3 dimensional sheared current [i.e. U(z), V(z), and W(z)] is calculated by solving for the balance of forces acting on it. The position of the top element (usually a floatation device) is solve for first, followed by each subsequent element until the bottom of the mooring is reached, which would usually be an anchor. The wire and chain elements are divided into 1 m "hinged" segments, so that the shape of the mooring will realistically represent a sub-surface mooring under the influence of a sheared current.

The code for the dynamics (MOORDYN.M) solves for the positions of each mooring element iteratively until the positions converge, usually only three iterations are required. The first pass (solution) starts with the mooring standing vertically in the water column. For subsurface moorings, it is assumed that the velocity data is sufficient to describe the currents throughout the water column, from the bottom (z=0) to a height that exceeds the vertical height of the mooring. Also, the velocity profile must have at least 3 values for interpolation. For surface moorings, the top (highest) velocity value defines the water depth, and this should be shallower than the slack current mooring length. The model will predict if the surface float will be "dragged" under the surface by the currents. Once the first order estimate of the "tilted" mooring has been made, a second solution is sought, with the new positions of each element in the sheared current. A third (and possibly subsequent) estimate(s) are made just in case the currents are severely sheared and small variations in the vertical position of the elements significantly alters the drag. If the position of the top element (float) moves less than 5 cm between iterations, then it is assumed the solution has converged and the position of the mooring has been found.

The solution assumes that each mooring element has a static force balance in each direction (x, y, and z). The forces acting in the vertical direction are: 1) Buoyancy [mass times g] positive upwards, i.e. floatation, negative downwards, i.e. an anchor, 2) Tension from above [Newtons], 3) Tension from below, and 4) Drag from any vertical velocity. In each horizontal direction, the balance of forces is simply: 1) Angled Tension from above, 2) Angled Tension from below, and 3) Drag from the horizontal velocity. The buoyancy is determined by the mass and displacement of the element and is constant. In MOORDESIGN.M the buoyancy is entered in [kg], and converted to a force in MOORDYN.M. The drag is determined for each element according to the shape, the exposed surface area of the element to the appropriate velocity component, and the drag coefficient (see below). Only cylinders and spherical shapes are assumed. More complicated shapes will have to be approximated by either a cylinder or a sphere with an appropriate (adjusted) drag coefficient.

For each element there are three equations and six unknowns (tension from above, tension from below, and the spherical coordinate angles the tensions make from the vertical (z) axis (psi) and in the x-y plane (theta). However, the top element has no tension from above and therefore, three unknowns and three equations. The tension and appropriate tension angles between any two elements is equal and acts in opposite directions, so that the tension from above for the lower element is equal and opposite to the tension and angles from below for the upper element. The method of solution is to estimate the lower tension and angles for the top element (floatation), and then subsequently estimate the tension and angles below each subsequent element. The resulting set of angles [psi(z) and theta(z)] and element lengths determines the exact (X, Y, Z) position of each mooring element relative to the anchor. Also, once the top of the anchor is reached, one has a direct estimate of the necessary tension required to "anchor" the mooring. This tension can then be inverted into an estimate of the required anchor weight. A Wood Hole (WHIO) safety factor is used to estimate a safe, realistic anchor weight.

Specifically, the solution is obtained as follows. First the velocity (current) profiles and wire/chain sections are interpolated to one metre vertical resolution using PINTERP.M, a parametric interpolation routine adapted from "Computers in Physics" [vol 8(6) p722]. Then the drag on each mooring element in the current is calculated by,

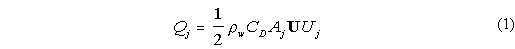
where Q_jis the drag in [N] on an element in water of density rho_w in the direction j (x, y, or z), U_j is the velocity component at the depth of the mooring element with a drag coefficient C_D appropriate for the shape of the element, with surface area A perpendicular to the direction j. U is the total vector magnitude of the velocity,

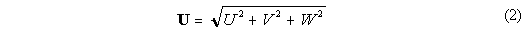
at the depth of the element. The drag in all three directions is estimated, even the vertical component which in most flows is likely to be very small.

Once the buoyancy and drag for each mooring element, and each metre of mooring wire and chain have been calculated, then the tension and the vertical angles necessary to hold that element in place (in the current) can be estimated. The three [x,y,z] component equations to be solved at each element are:

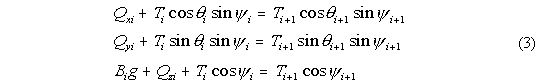
where T_i is the magnitude of the wire tension from above, making spherical angles psi_i and theta_i from the vertical and in the x and y plane, respectively, B_i is the buoyancy of the present element, g is the acceleration due to gravity (=9.81 ms^-2), and Q_xi, Q_yi and Q_zi are the respective drag forces. The tension below this element is T_i+1, with spherical coordinate angles psi_i+1 and theta_i+1. Thus each element acts dynamically as a "hinge" in the mooring, although it may be "rigid" in reality.

Once all of the angles have been calculated, the position of each element can be calculated using the length of each element, stored in array H(1,:) in MOORDESIGN.M and MOORDYN.M, namely
.

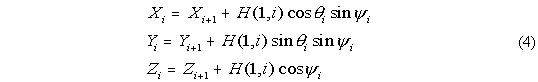The tilt of each element is taken into account when estimating the drag and surface area (1). In particular, the drag on a spheres require no direct modification except that the actual velocity acting on it corresponds to the velocity at the depth of the "tilted" mooring. For cylinder elements, once the mooring is tilting over, several modifications occur. First, the exposed area in the horizontal and vertical directions change. Also, the drag coefficient is reduced to C_Dcos³(phi), where the angles phi_x and phi_y are the angles from the vertical towards the X and Y axes, respectively. This holds for wire/rope/chain as well (which are treated as cylinder segments), with tilted wire having both a reduced area and drag coefficient to a horizontal current, but increased exposure and drag in the vertical.

The MATLAB routine MOORDYN.M can be used to "model" the mooring motion for a time dependant current. Although not included in the present Mooring Dynamics and Design package, it is easy to set up a "model" that cycles through a series of velocity profiles (i.e. a time series recorded by an Acoustic Doppler Current Profiler), and predicts the time history of each mooring element. These positions can then be animated as a time series, and even viewed as a movie to show the mooring motions in a dynamic environment (i.e. tidal channel). The present code does not estimate high frequency mooring motion, such as vibrations or strumming, although such calculations are possible given the Strouhal number 0.21= fd/U, where f is the frequency of vibration, d is the diameter of the cylinder element or wire, and U is the total speed past the device/wire.

Please report any errors or bugs, or suggested improvements for this package to RDewey@uvic.ca See the documentation file (moordesign.txt) for instructions on how to use the package, revisions and bugs, and future features being considered. I may also have a draft of the (J.Tech) technical paper available describing this package, it's use and the solutions it provides.
You are visitor since 1/12/98.
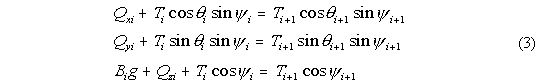
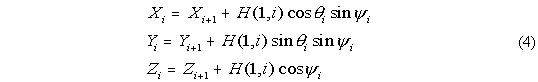